Langsung ke konten utama

Luas dan kelilin segi n beraturan

 

Luas Segi n Beraturan


 Sumber materi:https://supermatematika.com/luas-segi-n-beraturan

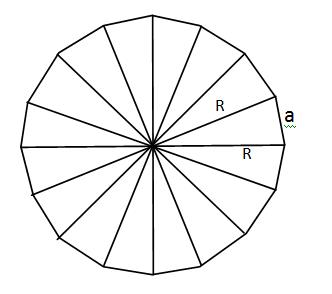
Pada segi n beraturan

Setiap segi n beraturan bisa kita bagi menjadi n buah segitiga yang kongruen

Setiap titik sudut pada segi n beraturan bisa dilalui sebuah lingkaran, lingkaran ini disebut lingkaran luar segi n. Semuat titik sudut akan dilewati lingkaran (tidak ada yang tertinggal).

 

Menghitung luas segi n beraturan akan lebih mudah jika diketahui jari-jari lingkaran luarnya

segi-n-beraturan

Setiap segi n bisa dibagi menjadi n buah segitiga yang kongruen seperti pada gambar di atas.

Selanjutnya kita ambil salah satu segitiganya

juring-segi-n

Besar sudut A adalah 

Luas segitiga adalah

LΔ = ½ .R.R sin A

Luas segi n beraturan adalah

Ln = n. LΔ

Rumus ini merupakan rumus luas segi n beraturan yang diketahui jari-jari lingkaran luarnya.

 

Bagaimana jika diketahui sisinya ?

Pertama kita cari dulu hubungan antara jari-jari lingkaran luar (R) dengan sisinya (a)

juring-segi-n

Dengan aturan cosinus maka

a2 = R2 + R2 — 2R.R cos A

a2 = 2R2 — 2R2 cos A

a2 = R2(2 — 2cos A)

Luas segi n :

luas-segi-n-beraturan

Jadi luas segi n beraturan yang panjang sisinya a adalah

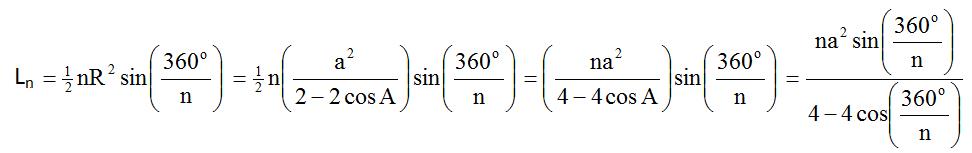
Komentar

Posting Komentar

Postingan populer dari blog ini

Limit

 LIMIT LIMIT Pada dasarnya, limit adalah suatu nilai yang menggunakan pendekatan fungsi ketika hendak mendekati nilai tertentu. Singkatnya, limit ini dianggap sebagai nilai yang menuju suatu batas. Disebut sebagai “batas” karena memang ‘dekat’ tetapi tidak bisa dicapai. Misalkan f adalah fungsi yang terdefinisi pada interval tertentu yang memuat a, kecuali di a itu sendiri, sedangkan L adalah suatu bilangan riil. Maka fungsi f dapat dikatakan memiliki limit L untuk x mendekati a, sehingga ditulis   Namun, hanya jika untuk setiap bilangan kecil ε > 0 terdapat bilangan δ > 0 sedemikian rupa sehingga jika 0 < |x-a| <δ maka |f(x)-L| <ε. Pernyataan tersebut dinamakan definisi limit secara umum. Rumus Limit Dalam ilmu matematika, konsep limit ini ditulis berupa:  Maksudnya, apabila x mendekati a tetapi x tidak sama dengan a, maka f(x) akan mendekati L. Pendekatan x ke a ini dapat dilihat dari dua sisi, yakni sisi kiri dan sisi kanan. Nah, dengan kata lain ba...
Posting Komentar
Baca selengkapnya

Sudut-sudut berelasi pada kuadran I,II,III,IV

 Sudut-sudut berelasi pada kuadran I,II,III,IV Sumber materi:https://www.danlajanto.com/2015/10/sudut-sudut-berelasi-trigonometri-sma_58.html?m=1 Perbandingan Trigonometri di Kuadran I Oleh karena pada gambar di atas, titik   M  (  x  1  ,   y  1  )   adalah bayangan dari titik   K  (  x  ,   y  )   oleh pencerminkan terhadap garis   y   =   x  , maka Dengan demikian, hubungan antara sudut   dengan   sudut   (90° - )   atau  ( π. 2 )  _  _  adalah sebagai berikut: Perbandingan Trigonometri di Kuadran II A. Sudut berelasi dengan sudut (180° - ) atau (π - ) Relasi antara sudut   dengan   sudut   (180° - )   adalah sebagai berikut: Perbandingan Trigonometri di Kuadran III A. Sudut berelasi dengan (180° + ) atau (π + ) Mari kita perhatikan gamba...
Posting Komentar
Baca selengkapnya

INTEGRAL FUNGSI ALJABAR

  𝗜𝗻𝘁𝗲𝗴𝗿𝗮𝗹, 𝗳𝘂𝗻𝗴𝘀𝗶 𝗮𝗹𝗷𝗮𝗯𝗮𝗿 INTEGRAL TAK TENTU   Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.  Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Nah, jika f’(x) dibalik lagi menjadi f(x), maka itu merupakan integral.  Sebelum ke rumus integral tak tentu, elo perlu paham konsep turunan nih. Gue kasih bayangin dikit tentang turunan secara umum. y= X3   Turunan dari soal ini berapa? dydx = 3×2  Setelah diturunkan seperti ini, lalu dikali silang. dy = 3×2 dx  d(X3) = 3×2 dx  Bisa dilihat ya, y diganti dengan X3 Nah, dari sini bisa kita simpulkan ya cara mencari turunan bentuknya akan seperti ini nih. Turunan dari X2 akan menjadi d(X2) = 2x dx Oke, konsep turunan udah ingat lanjut ke materi integral tak tentu lagi. Coba deh elo perhatikan antara turunan dan integral di bawah ini. Turunan: Sekarang kita balik, dikalikan si...
Posting Komentar
Baca selengkapnya